Para empezar, recordemos que el márgen es el coeficiente aplicado a un precio de coste para obtener un precio de venta. Habitualmente este coeficiente se expresa como un tanto por ciento aditivo sobre el coste:
precio-venta = precio-coste + precio-coste * %-margen / 100
precio-venta = precio-coste * (1 + %-margen / 100)
Márgenes lineales #
El caso más simple de margen es aquel que es constante para cualquier precio de coste. Es decir, que el % de márgen de la fórmula anterior no depende del precio de coste.
Básicamente, el márgen constante es lineal, y su representacion gráfica es una recta:

Si comparamos dos márgenes diferentes, vemos que cada uno de ellos es una recta cuya pendiente es proporcional al margen aplicado (a mayor margen, mayor pendiente):
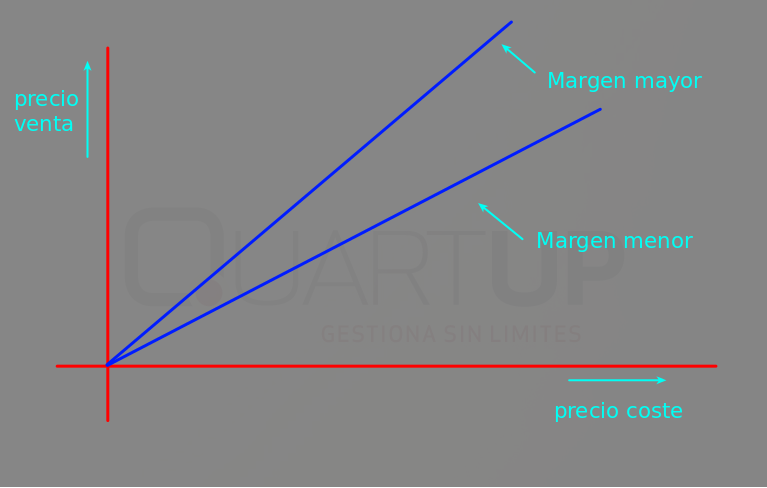
Márgenes variables #
Hay empresas en las que es suficiente un margen constante para todos los precios, pero es habitual que haya negocios en los que los márgenes deban variar según el coste inicial. En estos casos lo habitual es que el margen sea mayor para precios menores, y menor para precios mayores (esto se acostumbra a hacer para repercutir los costes fijos de la empresa de forma más racional, pero en este artículo no entraremos en estos detalles).
Márgenes escalables #
Antiguamente, cuando los márgenes se debían calcular manualmente, la forma más fácil de tener un margen variable era escalarlo según intervalos de precio orígen (por ejemplo: para costes inferiores a 10 euros aplicamos un 40% de margen, para costes entre 10 y 50 euros, aplicamos un 30% de margen, y para costes superiores a 50 euros aplicamos un 20% de margen).
Este formato nos genera una gráfica formada por segmentos de rectas discontinuos:
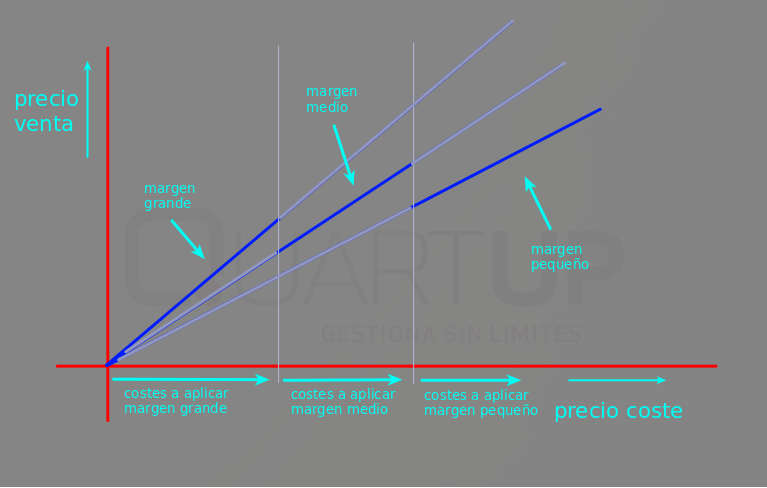
Este formato escalado tiene el inconveniente de que se produce un salto brusco en las zona de encaje de cada bloque, y esto puede ser un inconveniente muy grave en ciertas situaciones. Puede darse el caso, por ejemplo, en que al aplicar un cambio de tarifas de cambio de año, una pequeña subida en el precio de coste provoque que se salte al siguiente bloque del escalado, y se asigne un precio de venta considerablemente mayor al del año anterior.
Márgenes continuos pseudolineales #
Para evitar las discontinuidades de los márgenes escalables del punto anterior, podemos aplicar en la zona intermedia un margen lineal que nos empalme las dos rectas de márgenes máximo y mínimo, y así obtenemos un margen continuo, aunque anguloso:
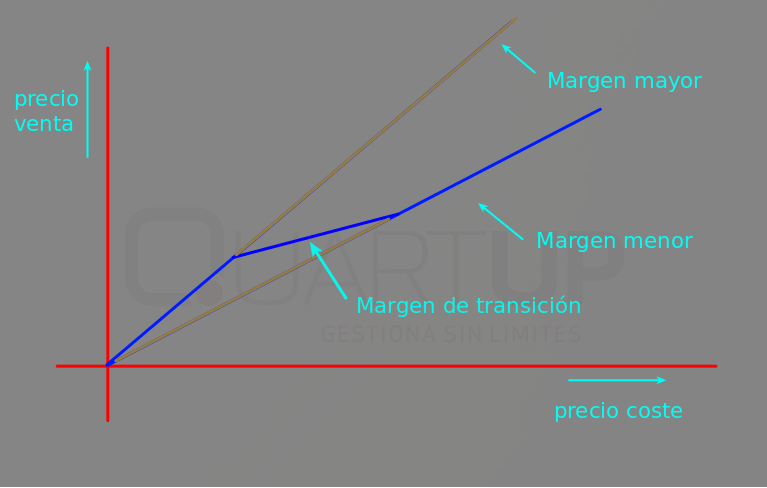
Este sistema es mejor que el escalable, pero tiene el pequeño inconveniente de que los puntos de encaje son angulosos, y generan una discontinuidad en la tasa de variación de los precios (la función es continua, pero no lo es la derivada).
Márgenes progresivos #
Para conseguir que los márgenes sean continuos, y que sus tasas de variación también lo sean, hemos de buscar una manera de poder empalmar las dos rectas de margen máximo y mínimo de forma suave, de manera que el margen aplicado a cada precio de coste vaya variando de forma paulatina en cada punto de la gráfica.
Gráficamente, lo que queremos es conseguir que la línea efectiva de los márgenes sea una curva suave que, en los extremos sea casi las dos rectas de los márgenes máximo y mínimo, y en el centro sea una transición sin abruptos entre ellas:
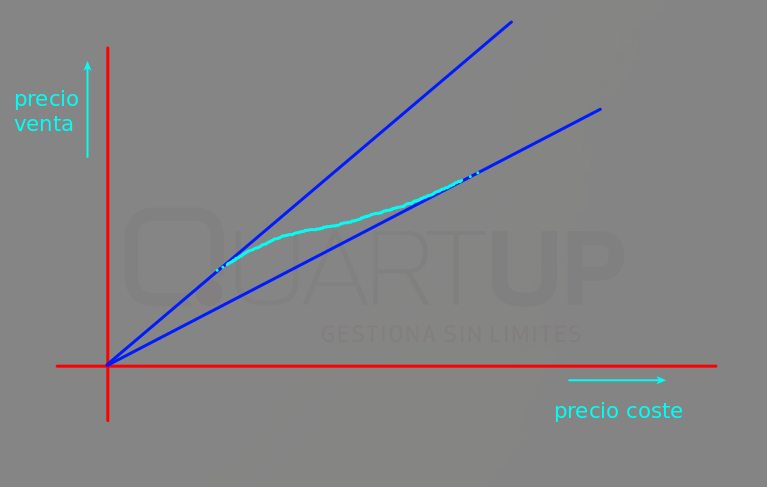
Para conseguir esta situación, hemos de aplicar un poco de matemáticas más elaboradas. Sin entrar en detalles, la forma analítica de conseguir una transición suave, es aplicar una ponderación entre las dos rectas mediante una función que sea asintótica a «1» en un extremo, y asintótica a «0» en el otro extremo.
Una de las funciones más simples que nos permite esta condición es la función «gaussiana» (básicamente, una exponencial del cuadrado de la variable), muy usada en distribuciones de probabilidad con el nombre «distribución normal» por ser el primer grado de aproximación de una distribución estadística simple.
Con esto, si aplicamos una ponderación gaussiana entre las dos rectas, obtenemos la siguiente expresión:
precio-venta =
precio-coste * (1 + %-margen-maximo / 100) * exp( – ? * precio-coste ² ) +
precio-coste * (1 + %-margen-minimo / 100) * (1 – exp( – ? * precio-coste ² ))
Donde todos los datos son conocidos, salvo el coeficiente «?» que es el que nos define la rapidez con que la gaussiana pasa de un extremo a otro.
Ahora solo nos queda concretar el parámetro «?» que tenemos libre en nuestra expresión. Como hemos dicho antes, «?» es el coeficiente que nos concreta la rapidez con que la gaussiana transita entre los dos extremos, y en definitiva este coeficiente hará que la etapa de transición entre el margen máximo y el mínimo se sitúe en una zona de precios o en otra, y por tanto, más arriba o más abajo en nuestra gama de precios.
Por esta razón, la manera más práctica de calcular «?» es que nos den el precio de coste donde queremos que se ubique el margen medio entre márgenes máximo y mínimo de partida. Por ejemplo: si nuestros márgenes máximo y mínimo son 40% y 20% respectivamente, entonces necesitamos que nos indiquen cual es el precio de coste al que queremos aplicar el 30% de margen.
Esto es lo que llamamos el «precio del punto medio«, y gráficamente es lo siguiente:
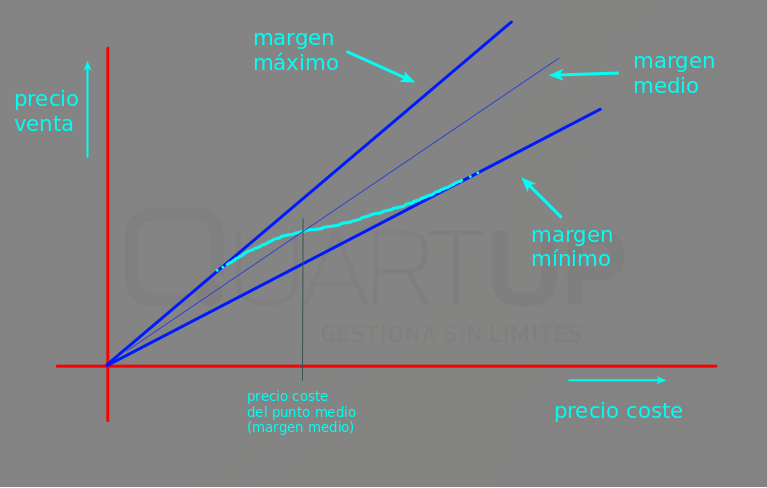
Por tanto, si nos dan el precio de coste sobre el cual hemos de aplicar el margen medio (precio del punto medio) entonces podemos calcular el coeficiente «?» y ya tendremos las fórmulas completas para hacer todos los cálculos.
Aplicando lo anterior, y para no atormentar a nuestro lectores con cálculos innecesarios, la fórmula final para los cálculos de los márgenes progresivos es la siguiente:
%-margen-progresivo =
%-margen-minimo
+ ( %-margen-máximo – %-margen-mínimo )
* 2 ** ( – (precio-coste / precio-punto-medio) ² )




